北海道の到達不能極を調べるコードをchatGPTと協力して作ってみた。
軽く調べた程度では北海道の到達不能極の場所はここ、という情報は見つけられなかった。
本州の到達不能極は長野県の佐久市にあるらしい。そこに設置してある看板によると「北海道の場合は石狩山地内で、海岸線からは108.2km離れている」とのこと。ちなみに佐久市の到達不能極は1996年9月に国土地理院によって計算されたそうだ。
計算に必要なデータを入手
日本の海岸線のデータは国土交通省の「国土数値情報ダウンロードサイト」というところで公開されている。海岸線データは非商用であれば利用できる。最新のデータは2025年8月時点で、2006年度に作成されたものとなっている。
国土数値情報ダウンロードサイト 海岸線データ
https://nlftp.mlit.go.jp/ksj/gml/datalist/KsjTmplt-C23.html
計算には測地系や測地線距離の知識が必要。測地系については下記の国土地理院のページが参考になった。
国土地理院 日本の測地系
https://www.gsi.go.jp/sokuchikijun/datum-main.html
また、使用した地理情報ライブラリについては下記のサイトの内容を参考にさせて頂いた。
いかたこのたこつぼ pyproj
https://ikatakos.com/pot/programming/python/packages/pyproj
以降に登場する図は、「国土数値情報(海岸線データ)」(国土交通省, 北海道)
https://nlftp.mlit.go.jp/ksj/gml/datalist/KsjTmplt-C23.html (2025年6月17日取得)
を加工して作成したものです。
一つ目のコード
計算方法が違う二つのコードを作成した。とりあえず両方載せておくことにする。
一つ目のものはGoogle Colabで実行するものを作った。変数の命名とか書き方がめちゃくちゃなのは許してほしい。
生成AIで作ったコードの著作権とかはよくわからないが、無断転載とか自作発言等はご遠慮ください。
!pip install japanize-matplotlib
import geopandas as gpd
from shapely.geometry import LineString, Polygon, MultiPolygon, Point
from shapely.ops import polygonize, unary_union
from shapely.strtree import STRtree
import numpy as np
from pyproj import Geod
import matplotlib.pyplot as plt
import japanize_matplotlib
from google.colab import files
# 測地線距離を扱うインスタンス
geod = Geod(ellps='GRS80')
#ファイルのアップロード
print("C23-06_01-g_Coastline をアップロードしてください")
uploaded = files.upload()
# 海岸線のShapefile読み込み
coastline_gdf = gpd.read_file("C23-06_01-g_Coastline.shp")
# 全てのLineStringを1つに統合
merged_lines = unary_union(coastline_gdf.geometry)
# polygonizeで閉じたポリゴンを生成
polygons = list(polygonize(merged_lines))
# ポリゴンをGeoDataFrameに変換
land_gdf = gpd.GeoDataFrame(geometry=polygons, crs="EPSG:4612")
# 結果の確認
land_gdf.plot()
# ───── 北海道内部の 10km グリッドで計算 ─────
minx, miny, maxx, maxy = land_gdf.total_bounds
x_coords = np.arange(minx, maxx, 0.1) # 約10km
y_coords = np.arange(miny, maxy, 0.1)
'''
# ───── 計算範囲を手動で指定する場合 ─────
# 経度[°]
minx = 142.803283 - 0.00001
maxx = 142.803283 + 0.00001
# 緯度[°]
miny = 43.442535 - 0.00001
maxy = 43.442535 + 0.00001
# グリッド点間隔[°]
x_coords = np.arange(minx, maxx, 0.000001) # 約0.1m
y_coords = np.arange(miny, maxy, 0.000001)
'''
land_union = land_gdf.geometry.union_all()
points = []
for x in x_coords:
for y in y_coords:
p = Point(x, y)
if land_union.contains(p):
points.append(p)
print(f"北海道内に生成されたグリッド点の数: {len(points)}")
#グリッド点をGeoDataFrameに変換
grid_gdf = gpd.GeoDataFrame(geometry=points, crs="EPSG:4612")
#描画
fig, ax = plt.subplots(figsize=(10, 10))
land_gdf.plot(ax=ax, color='lightgreen', edgecolor='black')
grid_gdf.plot(ax=ax, color='blue', markersize=1)
ax.tick_params(labelsize=15)
ax.set_aspect('equal')
plt.title("北海道内に生成された10kmグリッド点", fontsize=20)
plt.xlabel("経度", fontsize=20)
plt.ylabel("緯度", fontsize=20)
plt.grid(True)
plt.show()
# ───── 最遠点を探す ─────
max_dist = 0
farthest_point = None
nearest_point = None
for i, point in enumerate(points):
if i % 100 == 0:
print(f"{i} / {len(points)} 点目を処理中…")
min_dist = float("inf")
nearest = None
for coast in coastline_gdf.geometry:
candidate = coast.interpolate(coast.project(point))
lon1, lat1 = point.x, point.y
lon2, lat2 = candidate.x, candidate.y
_, _, dist = geod.inv(lon1, lat1, lon2, lat2)
if dist < min_dist:
min_dist = dist
nearest = candidate
if min_dist > max_dist:
max_dist = min_dist
farthest_point = point
nearest_point_on_coast = nearest
# ───── 結果出力 ─────
print("\n📍 到達不能極の緯度経度(10kmグリッドで計算):")
print(f" 緯度: {farthest_point.y:.6f}")
print(f" 経度: {farthest_point.x:.6f}")
print(f" 最短距離: {max_dist/1000:.3f} km")
print("\n🌊最近接の海岸線上の点:")
print(f" 緯度: {nearest_point_on_coast.y:.6f}")
print(f" 経度: {nearest_point_on_coast.x:.6f}")
#地図にプロット
fig, ax = plt.subplots(figsize=(10, 10))
land_gdf.plot(ax=ax, color="lightgreen", edgecolor="black")
#coastline.plot(ax=ax, color="blue")
gpd.GeoSeries(farthest_point).plot(ax=ax, color="red", marker="*", markersize=100, label="到達不能極")
gpd.GeoSeries(nearest_point_on_coast).plot(ax=ax, color="orange", marker="o", markersize=60, label="最近接海岸点")
#赤い線を引く
line = LineString([farthest_point, nearest_point_on_coast])
gpd.GeoSeries(line).plot(ax=ax, color="red", linestyle="--", linewidth=2, label="最短経路")
ax.tick_params(labelsize=15)
ax.set_aspect('equal')
plt.title("北海道の到達不能極と最近接の海岸点(10kmグリッドで計算)", fontsize=20)
plt.xlabel("経度", fontsize=20)
plt.ylabel("緯度", fontsize=20)
plt.grid(True)
plt.legend(fontsize=20)
plt.show()1.必要なライブラリの準備
地図描画で日本語を扱えるように japanize-matplotlib をインストール。続いて地理系のライブラリをインポート。
測地線距離(楕円体上での最短距離) を扱うために、楕円体を GRS80 で設定している。参照した海岸線データが日本測地系(JGD2000)のため、それに合わせている。
geod = Geod(ellps='GRS80')2. 海岸線データの読み込み
北海道の海岸線を Shapefile から読み込む。Google Colab では files.upload() を使って手元のファイルをアップロードできる。
アップロードするファイルは、
C23-06_01-g_Coastline.dbf
C23-06_01-g_Coastline.shp
C23-06_01-g_Coastline.shx
の三つ。
その後、海岸線から北海道のポリゴン(面)を作ってGeoDateFrameに変換する(land_gdf)。これにより北海道の陸地の領域を扱うことができる。EPSG:4612というのは座標系などを示すコードで、4612は測地系がJGD2000、準拠楕円体がGRS80、投影座標系が緯度経度であることを表している。
uploaded = files.upload()
coastline_gdf = gpd.read_file("C23-06_01-g_Coastline.shp")
# 全てのLineStringを1つに統合
merged_lines = unary_union(coastline_gdf.geometry)
# polygonizeで閉じたポリゴンを生成
polygons = list(polygonize(merged_lines))
# ポリゴンをGeoDataFrameに変換
land_gdf = gpd.GeoDataFrame(geometry=polygons, crs="EPSG:4612")3.北海道全域にグリッド点を生成
北海道の範囲を求め、その内部に 任意の間隔のグリッド点 を配置する。
minx, miny, maxx, maxy = land_gdf.total_bounds
x_coords = np.arange(minx, maxx, 0.1) # 約10km
y_coords = np.arange(miny, maxy, 0.1)4.最遠点(到達不能極)の探索
各グリッド点から海岸線までの最短距離を計算し、もっとも海から遠い点 を探す。
距離計算には pyproj.Geod.inv() を使って、緯度経度のペアから測地線距離を求めている。
処理の流れ:
- グリッド点ごとに最近接の海岸線上の点を探す
- その点までの距離を測地線で計算
- 最大値を更新していき、最遠点を記録
max_dist = 0
farthest_point = None
nearest_point = None
for i, point in enumerate(points):
if i % 100 == 0:
print(f"{i} / {len(points)} 点目を処理中…")
min_dist = float("inf")
nearest = None
for coast in coastline_gdf.geometry:
candidate = coast.interpolate(coast.project(point))
lon1, lat1 = point.x, point.y
lon2, lat2 = candidate.x, candidate.y
_, _, dist = geod.inv(lon1, lat1, lon2, lat2)
if dist < min_dist:
min_dist = dist
nearest = candidate
if min_dist > max_dist:
max_dist = min_dist
farthest_point = point
nearest_point_on_coast = nearest緯度経度の小数点以下6桁まで計算すると以下の結果が得られた。計算には20分ほどかかった。最短経路はただの直線で結んでいるだけ。
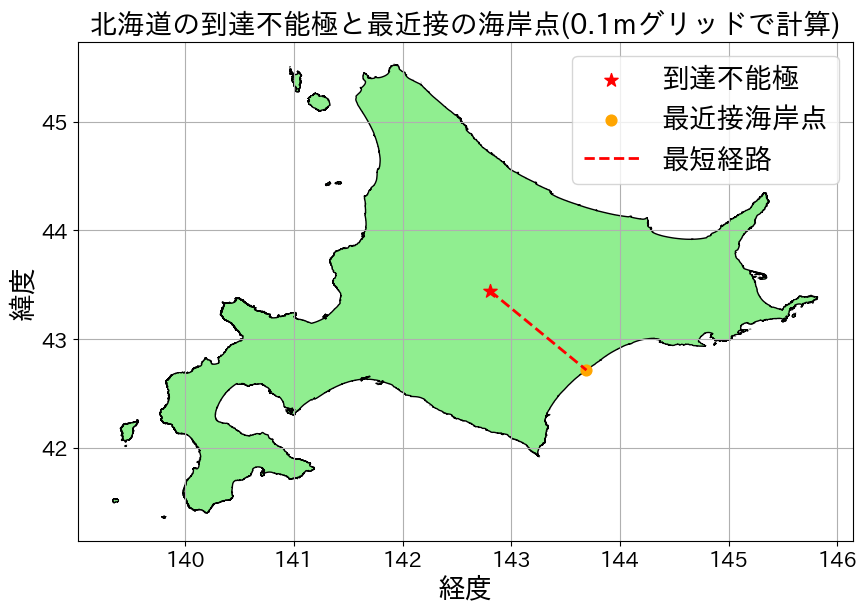
📍 到達不能極点の緯度経度(0.1mグリッドで計算):
緯度: 43.442535
経度: 142.803283
最短距離: 108.593 km
🌊最近接の海岸線上の点:
緯度: 42.712966
経度: 143.690753
この結果が正しいか検証するために、QGISにて北海道の海岸線、座標142.803283, 43.442535を中心とした半径108.593kmの円をプロットして確認する。座標参照系はEPSG:4612 – JGD2000でそろえている。
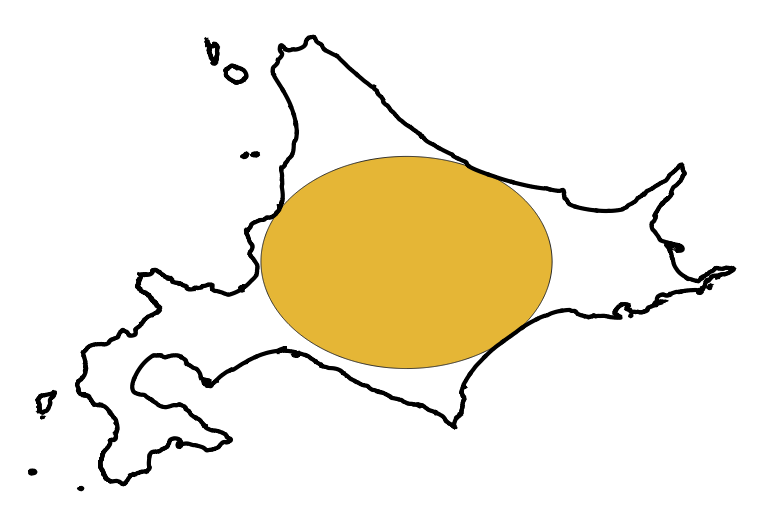
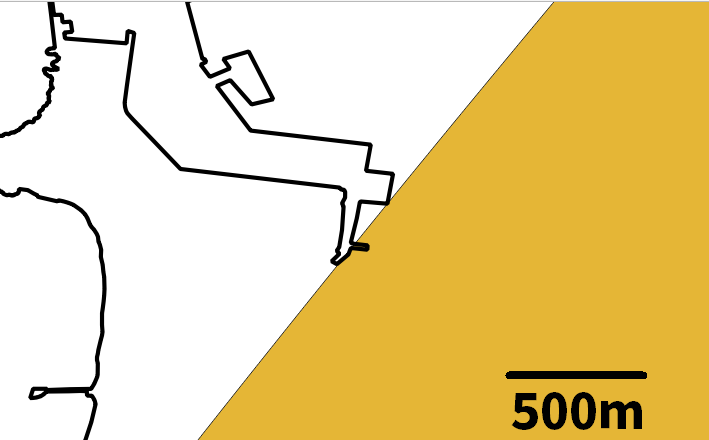
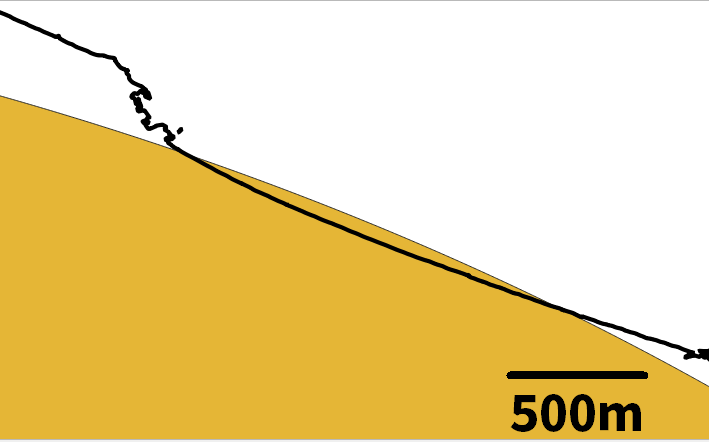

半径108.593kmの円は留萌、紋別、浦幌の海岸線と接していることがわかるが、拡大してみるとずれている。
各グリッド点から最近接の海岸の地点を以下の方法で取得しているが、おそらくうまくいっていないと思われる。
candidate = coast.interpolate(coast.project(point))二つ目のコード
各グリッド点から最近接の海岸の地点をより厳密に求めることにする。今度はGoogle ColabではなくThonnyというPython IDEで動かしている。
流れとしては、各グリッド点から半径が測地線距離の円を作成して、海岸線と交差判定が出るまで徐々に大きくしていく。このときの座標と半径を記録して到達不能極を求める。
import geopandas as gpd
from shapely.geometry import Point
from shapely.ops import polygonize, unary_union
from pyproj import Geod
import numpy as np
from tqdm import tqdm
import matplotlib.pyplot as plt
import matplotlib.patches as mpatches
import matplotlib.lines as mlines
# 日本語フォント
plt.rc('font', family='BIZ UDGothic')
# 測地線計算用楕円体設定(GRS80)
geod = Geod(ellps="GRS80")
# 海岸線Shapefileの読み込み
coastline_gdf = gpd.read_file("C23-06_01-g_Coastline.shp")
# 計算範囲とグリッド間隔(0.01 → 約1km間隔)
min_lat, max_lat = 43.438901 - 0.00001, 43.438901 + 0.00001
min_lon, max_lon = 142.798450 - 0.00001, 142.798450 + 0.00001
lat_step, lon_step = 0.000001, 0.000001
# 探索パラメータ
initial_radius = 108410
radius_step = 0.1
max_radius = 115000
# 結果格納用
max_distance = 0
farthest_point = None
farthest_circle_geom = None
grid_results = []
farthest_intersection = None
# グリッド点生成(境界点含む)
lat_grid = np.arange(min_lat, max_lat + lat_step / 2, lat_step)
lon_grid = np.arange(min_lon, max_lon + lon_step / 2, lon_step)
for lat in tqdm(lat_grid, desc="緯度スキャン"):
for lon in lon_grid:
origin = Point(lon, lat)
found = False
radius = initial_radius
current_intersection = None # この点での交点
while radius <= max_radius:
# 方位ごとに円周点を生成
circle_points = []
for azimuth in np.linspace(0, 360, 36000):
lon2, lat2, _ = geod.fwd(lon, lat, azimuth, radius)
circle_points.append(Point(lon2, lat2))
circle_geom = gpd.GeoSeries(circle_points, crs="EPSG:4612").union_all().convex_hull
if coastline_gdf.intersects(circle_geom).any():
found = True
# 交点を記録(GeometryCollectionになることもある)
intersection = coastline_gdf.intersection(circle_geom)
intersection = intersection.dropna()
current_intersection = intersection.union_all()
break
radius += radius_step
if found:
grid_results.append((lat, lon, radius))
if radius > max_distance:
max_distance = radius
farthest_point = Point(lon, lat) # ← 正しくPoint型にする
farthest_circle_geom = circle_geom
farthest_intersection = current_intersection
print("到達不能極:", farthest_point)
print("最短距離:", max_distance, "m")
print("最近接海岸点:", farthest_intersection)
# =====================
# 描画
# =====================
fig, ax = plt.subplots(figsize=(10, 10))
# 海岸線
coastline_gdf.plot(ax=ax, color='black')
# 最遠点の円(赤)
gpd.GeoSeries([farthest_circle_geom]).plot(ax=ax, facecolor='none', edgecolor='red', linewidth=2)
# 最遠点マーカー(赤の星)
gpd.GeoSeries([farthest_point]).plot(ax=ax, color='red', marker='*', markersize=100)
#最近接海岸点
gpd.GeoSeries([farthest_intersection]).plot(ax=ax, color='orange', marker='o', markersize=100)
#mpatches.Patch(color='lightblue',label='海岸線'),
# カスタム凡例
legend_handles = [
mlines.Line2D([], [], color='red', marker='*', linestyle='None', markersize=15, label='到達不能極'),
mlines.Line2D([], [], color='orange', marker='o', linestyle='None', markersize=15, label='最近接海岸点'),
mlines.Line2D([], [], color='red', linewidth=2, label='最近接距離の円')
]
ax.legend(handles=legend_handles, fontsize=15)
# 軸・凡例・タイトル
ax.tick_params(labelsize=15)
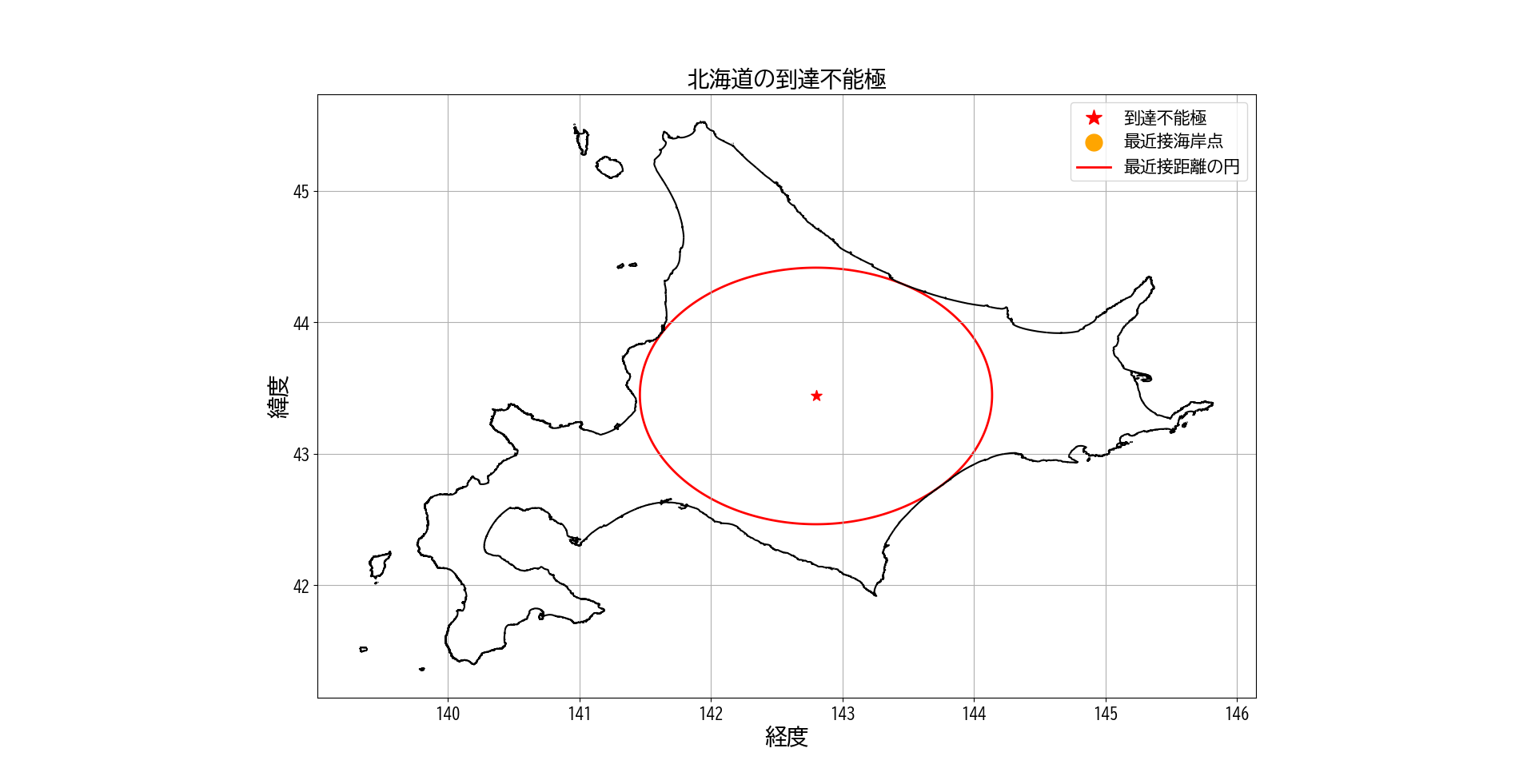
ax.set_title("北海道の到達不能極", fontsize=20)
plt.xlabel("経度", fontsize=20)
plt.ylabel("緯度", fontsize=20)
plt.grid(True)
plt.show()1.ライブラリの準備
GeoPandas / Shapely : 地理情報データ(海岸線や点・ポリゴン)を扱う
Pyproj (Geod) : 楕円体上での測地線距離(地球の曲率を考慮した距離)を計算する
tqdm : グリッド探索の進行状況を表示するプログレスバー
matplotlib : 結果を可視化
日本語フォントも設定。
import geopandas as gpd
from shapely.geometry import Point
from shapely.ops import polygonize, unary_union
from pyproj import Geod
import numpy as np
from tqdm import tqdm
import matplotlib.pyplot as plt
import matplotlib.patches as mpatches
import matplotlib.lines as mlines
# 日本語フォント
plt.rc('font', family='BIZ UDGothic')2.海岸線データの読み込み
Shapefile から 北海道の海岸線 を読み込む。
coastline_gdf = gpd.read_file("C23-06_01-g_Coastline.shp")3.探索範囲とグリッド点の準備
探索する中心の座標と範囲を指定する。そしてグリッド点の間隔も指定。
min_lat, max_lat = 43.438901 - 0.00001, 43.438901 + 0.00001
min_lon, max_lon = 142.798450 - 0.00001, 142.798450 + 0.00001
lat_step, lon_step = 0.000001, 0.000001 次に探索パラメータを設定。探索円の開始半径と増加ステップ、探索を打ち切る最大半径を設定する。
開始半径をなるべく大きくすると計算にかかる時間を短縮できる。
initial_radius = 108410 # 開始半径[m]
radius_step = 0.1 # 半径を増加させるステップ[m]
max_radius = 115000 # 最大半径[m](探索打ち切り)4.各グリッドでの探索と円の拡張
各グリッド点を中心として、半径 radius の円を描き、その円が海岸線と交わるかどうかを調べる。円が海岸線と交わった時の半径を「その地点から海岸までの最短距離」とする。円がまだ海岸線に届いていない場合、半径を少しずつ広げていき、交わるまで繰り返す。
ここでポイントとなるのが円の描き方。地球は球面なので単純に円を描くのは難しい。そこでgeod.fwd()を使う。
geod.fwd(lon, lat, azimuth, distance)は PyProj ライブラリに含まれる関数で「ある地点(緯度・経度)から、指定した方位角の方向に、指定した距離だけ進んだ地点の座標を計算する」もの。
例えば「北緯43°, 東経142°から、東へ1km進むとどこに着く?」を計算してくれるイメージ。
実際のコードでは、0°から360°までの方位角を 0.01°刻み(= 36,000点) で少しずつ変えながらgeod.fwd()を呼び出し、円周上の点を1つずつ求めている。その点をすべてつなぎ合わせることで「円に近い多角形」を作っている。そのため処理にかなり時間がかかるがそれは仕方ない。
for lat in tqdm(lat_grid, desc="緯度スキャン"):
for lon in lon_grid:
origin = Point(lon, lat)
radius = initial_radius
while radius <= max_radius:
# 方位角ごとに円周点を生成
circle_points = []
for azimuth in np.linspace(0, 360, 36000):
lon2, lat2, _ = geod.fwd(lon, lat, azimuth, radius)
circle_points.append(Point(lon2, lat2))
circle_geom = gpd.GeoSeries(circle_points, crs="EPSG:4612").union_all().convex_hull
# 海岸線と交差したら終了
if coastline_gdf.intersects(circle_geom).any():
intersection = coastline_gdf.intersection(circle_geom).dropna().union_all()
...
break
radius += radius_step
緯度経度の小数点以下6桁まで計算したものがこちら。ひとつ目のコードで求めた地点の周囲1kmの範囲で計算した。筆者の環境では計算に半日かかった。
到達不能極: POINT (142.798448 43.438896)
最短距離: 108413 m
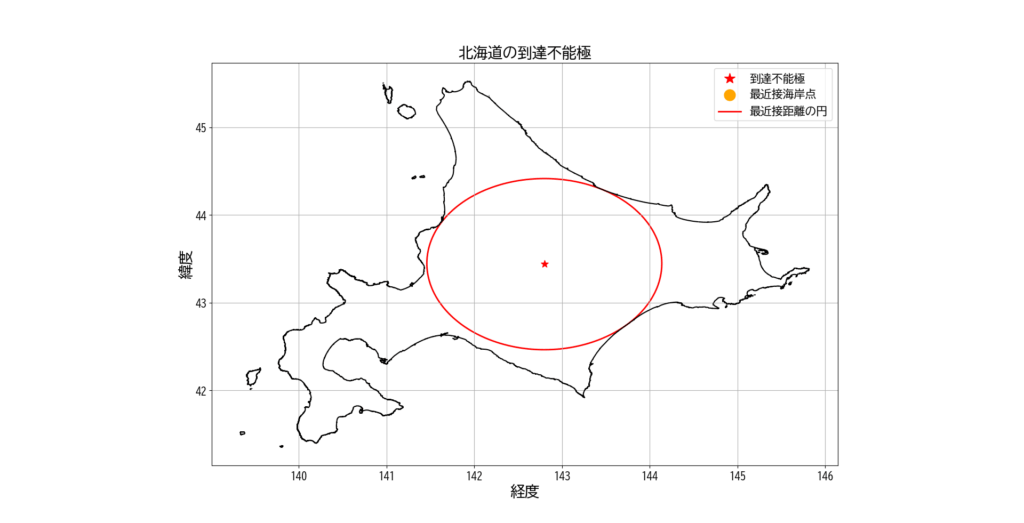
先ほどと同様にQGISにて北海道の海岸線と、座標142.798448, 43.438896を中心とした半径108.413kmの円をプロットして確認する。
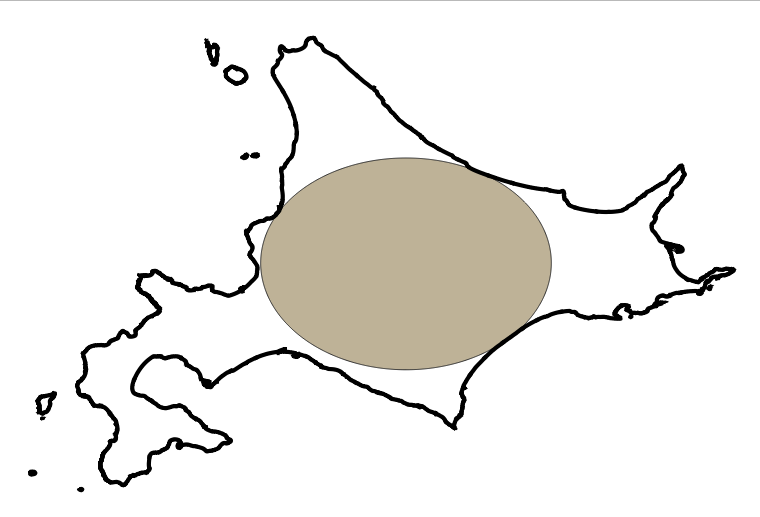
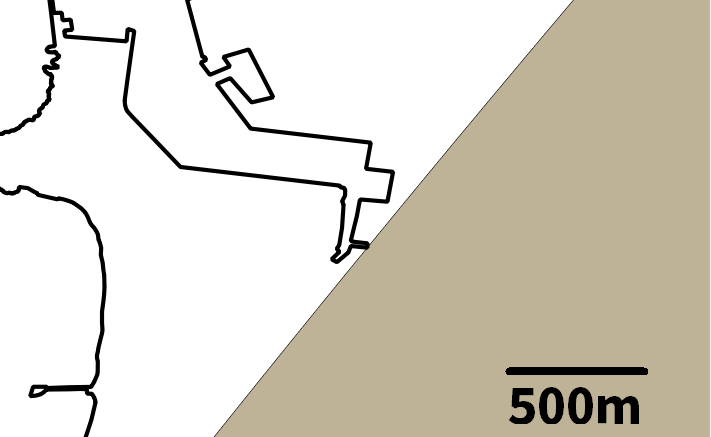
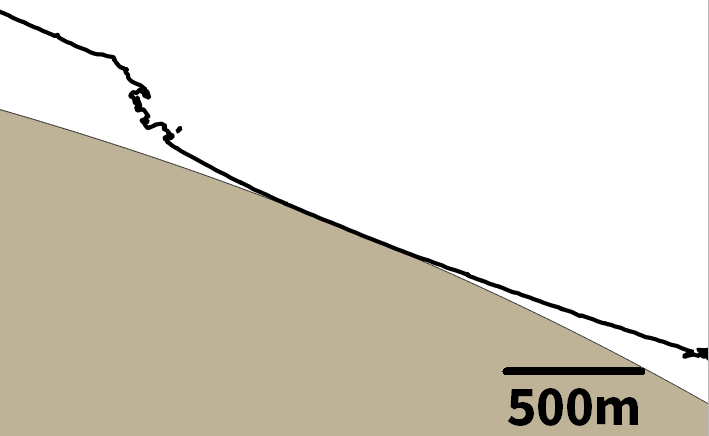
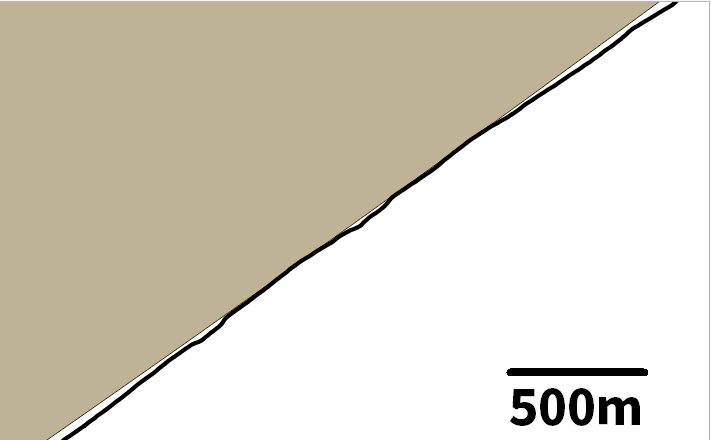
ひとつ目のコードの結果よりも誤差は小さくなったように見える。少なくとも誤差は1m以内には収まっていると思う。
まとめ
北海道の到達不能極をPythonで求めた。結果は以下の通り。
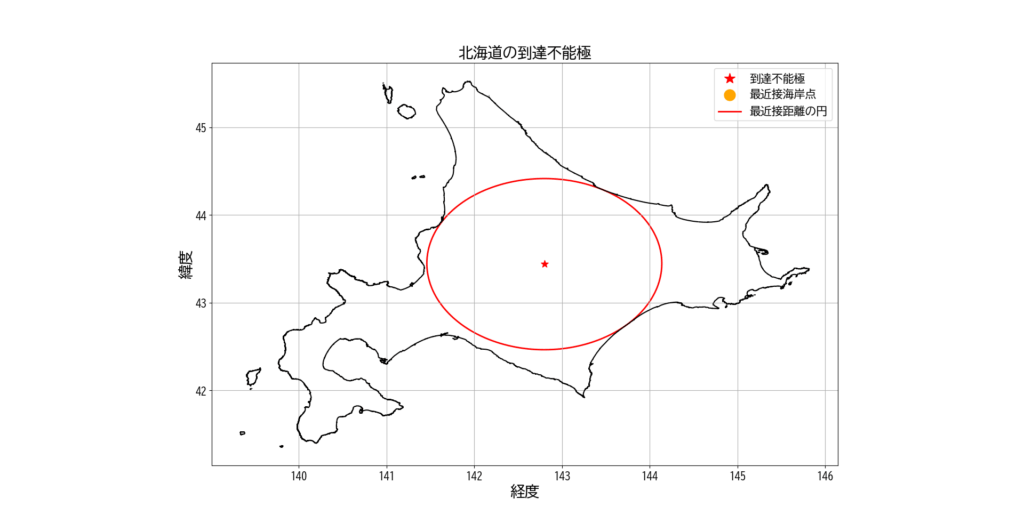
- 東経142.798448°, 北緯43.438896°
- 海岸線まで108.413km
これだけの計算が個人で、かつ無料でできるとは… いい時代になったものだ。
筆者は地理計算については完全に素人なのでもしかしたら間違っているかもしれないが、ひとまずこれで終了とする。この方法で本州の到達不能極を計算してみたり、四国、九州で計算しても面白いかもしれない。
計算した到達不能極の近くをツーリングしてみた動画を公開しているので、よろしければご覧ください。
https://www.nicovideo.jp/watch/sm45308838